Um meine JavaScript-Kenntnisse zu vertiefen, habe mich daran gemacht einen Graphen aus Knoten und Kanten zu implementieren. Und weil das zu einfach ist, soll darauf das Traveling Salesman Problem gelöst werden :)
Für das TSP werden eine Reihe von Punkten (z.B. Städte auf einer Landkarte, können aber auch dreidimensional sein) sortiert. Aber nicht einfach irgendwie, sondern so dass beim Durchgehen der Punkte von einem zum nächsten die zurückgelegte Strecke möglichst kurz ist. Wie ein Handelsreisender, der Benzin sparen möchte, daher der Name. Das Problem ist für die Informatik interessant, weil es überraschend schwer ist, es optimal zu lösen. Ein Computer muss bei jedem einzelnen Punkt nämlich erstmal alle anderen Punkte prüfen und schauen, wo der neue an besten hinpasst. Bei vielen Punkten kann die Rechenzeit für eine optimale Lösung mehr Zeit in Anspruch nehmen, als z.B. das Universum existiert. Die Klasse der Probleme, zu der das TSP gehört wird von Profis daher auch “die echt richtig schweren Probleme” genannt. Allerdings ist das Problem nicht nur rein akademisch, sondern unter anderem für Logistik-Unternehmen relevant, also für den Post- oder Hermesboten oder für Containerschiffe. Die benutzen für ihre Tourenoptimierung dann keine optimalen Lösungen (keine Zeit), sondern Annäherungen, die “gut genug” sind. Und da gibt es einen ganzen Sack von Strategien, die ausgesprochen spannend sind - natürlich für eine ganz persönliche Definition von “spannend” :-D
An einige Algorithmen dazu kann ich mich noch ganz gut aus meinem Studium erinnern, aber ehrlich gesagt habe ich nicht so viel Lust, die alten Unterlagen nochmal herauszukramen. Glücklicherweise kann man Inspiration bei the Project Spot finden. Diese Implementierung muss dann ja nur noch nach JavaScript portiert werden.
Im Kern besteht die Idee darin, paarweise zufällig gewählte Kanten einer Tour zu vertauschen und zu prüfen, ob das Ergebnis besser ist als die bislang beste Tour. Die Wahrscheinlichkeit, dass eine schlechtere Lösung akzeptiert wird (um ein lokales Minimum zu vermeiden) ist direkt abhängig von der “Temperatur”.
Ausgangspunkt ist eine zufällige Tour.
function acceptanceProbability(energy,
newEnergy,
temperature) {
// If the new solution is better, accept it
if (newEnergy < energy) {
return 1.0;
}
// If the new solution is worse,
//calculate an acceptance probability
return Math.exp(
(energy - newEnergy) / temperature);
}
Nach jedem Durchgang verringert sich die Temperatur und wenn sie unter 1 gefallen ist, wird das bis dahin beste Ergebnis akzeptiert, daher “Simulated Annealing” - simulierte Erstarrung.
function solve() {
// Set initial temp
var temp = 10000,
// Cooling rate
coolingRate = 0.001;
...
while (temp > 1) {
...
// Cool system
temp *= 1 - coolingRate;
}
}
Drumherum schwirrt noch ein ganzer Sack Code, der für die Liste der Punkte, die Berechnung der euklidischen Distanz zwischen zwei Punkten, die aktuelle Tour, ihre Gesamtlänge und noch viel mehr zuständig ist:
...
function distanceTo (point, otherPoint) {
var xDistance = Math.abs(point.x - otherPoint.x),
yDistance = Math.abs(point.y - otherPoint.y),
// Skip Math.sqrt - real distance is not
// important, as long as relative distance
// is correct. And it's soo slow!
distance = (xDistance * xDistance)
+ (yDistance * yDistance);
return distance;
}
...
Der ganze Kladderadatsch wird dann mit einem Array von Punkten gefüttert und gestartet:
var points = [
{x: 60, y: 200},
{x: 180, y: 200},
{x: 80, y: 180},
{x: 140, y: 180},
{x: 20, y: 160},
{x: 100, y: 160},
{x: 200, y: 160},
{x: 140, y: 140},
{x: 40, y: 120},
{x: 100, y: 120},
{x: 180, y: 100},
{x: 60, y: 80},
{x: 120, y: 80},
{x: 180, y: 60},
{x: 20, y: 40},
{x: 100, y: 40},
{x: 200, y: 40},
{x: 20, y: 20},
{x: 60, y: 20},
{x: 160, y: 20}
];
halfdane.tsp.createAnnealing(points).solve();
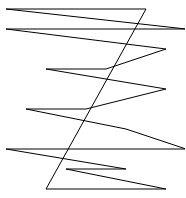
Insgesamt würde ich beim Anschauen des Ergebnisses sagen: ja, es funktioniert, aber mit den paar Punkten hätte ich das auch manuell machen können.

Bei größeren Punktmengen (z.B. 100 Punkte) wird die Rechenzeit schon seeehr lang und das Ergebnis ist trotzdem nicht so richtig beeindruckend:
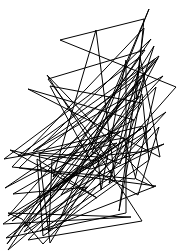
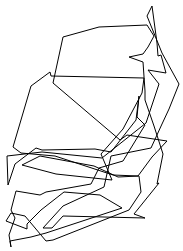
… und das waren jetzt wirklich nur nur 100 Punkte. Ich wollte eigentlich eher 20-mal so viele. Und das soll auf einem Handy laufen, nicht auf einer Workstation :/ Tja, nicht umsonst gehört das TSP zu der Klasse der echt richtig schwierigen Probleme :).
[UPDATE 19.1.2014]
Ich habe den Code jetzt mal eingebunden und eine Live-Demo vorbereitet - mit 20 Punkten, damit es nicht so lange dauert. Tut es natürlich trotzdem :P
Die Ausgabe ist zunächst die initiale Tour und dann bei jeder Verbesserung ein weiteres Bild. Unten im Bild wird die aktuelle Temperatur angezeigt.
Click zum Start
Der zugehörige Code ist hier verfügbar:
